The maximum power theorem, better known as the maximum power transfer theorem, is an essential tool for ensuring successful system design. Put simply, this theorem states that the maximum power that can be transferred from source to load is 50%, which occurs when source impedance is exactly matched to load impedance. The theorem is not as simple as it seems at first glance, however, and can be easily misunderstood.
In fact, James Prescott Joule himself did not completely understand the theorem. During the initial design of the modern-day motor, he said that the power delivered to the electric motor would always be the same as the heat lost in the system and, thus, could never achieve more than 50% operational efficiency. While he was correct in his first statement, he was off the mark in his deduction about the efficiency of the motor. In reality, maximum efficiency of the motor — or any circuit under the maximum power transfer condition of impedance matching — is 50%, but this is not the maximum possible efficiency. Higher efficiency can be achieved.
It was Thomas Edison who realized maximum power transfer and maximum efficiency are different entities. If load resistance is increased, higher efficiency can be achieved. Efficiency is the percentage of input power that is dissipated in the load. The maximum power transfer theorem tells us the load resistance, which will get maximum magnitude of power delivered to it by the source. However, input power from the source depends on load; if load resistance is increased, overall power decreases in magnitude, but the percentage of input power transferred to load increases. In other words, when load resistance increases, more power is dissipated in the load than in the source impedance, Hence, efficiency is increased. The magnitude of overall power is decreased, however, due to the increased resistance. Similarly, if load resistance is decreased, a lower percentage of total input power is dissipated in the load, and efficiency decreases.
The maximum power transfer theorem deals with matching impedance. And while it aids in the design of efficient circuits, it does not coincide with maximum power input efficiency at all. So why do we need impedance matching? Let’s have a look at the details.
The Basics of the Maximum Power Transfer Theorem
The purpose of the maximum power theorem is to find the optimal ratio of load impedance to source impedance for the purpose of power transfer. The theorem essentially states that the maximum magnitude of power — not efficiency, which is the ratio — will be dissipated by a load resistance when said resistance is equal to the Thevenin-Norton resistance of the power-supplying network. When the voltage and magnitude of internal resistance of the source are fixed, sometimes it is ideal to have the maximum magnitude of power transferred to the load at the expense of optimal efficiency. When power is limited, it’s critical to transfer as much as possible, and impedance matching is essential.
Relevant Tables and Formulas
When established as a mathematical problem and expressed in Ohm’s Law equations, maximum power transfer looks like this:
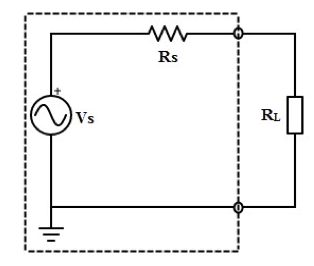
The Vs and Rs are the Thevenin-equivalent voltage and resistance of the source, respectively. RL is the load resistance. Current through the load is
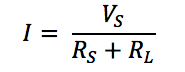
Power dissipated in the load is given by:
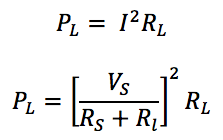
Since Vs and Rs are Thevenin equivalents and constant power depends on RL. To find the value of RL for which power is maximized, the above expression is differentiated with respect to RL and then equated to zero. The value obtained for RL is:
![]()
So, power dissipated in the load is at a maximum when load resistance equals source resistance. Or, when we talk about AC circuits, we say load impedance is equal to the complex conjugate of source impedance.
Practical Applications: Matching Conditions
In practical applications, it’s generally safe to apply a rule of matched conditions: An active device, or power supply, transfers maximum power to an external device when said device’s impedance is matched exactly to the impedance of the source supply.
For day-to-day applications, this is useful when the maximum possible magnitude of power must be transferred from a fixed source. For systems in which input voltage does not normally change and maximum power transfer is required, achieving maximum efficiency is not important. For example, the impedance of an amplifier is matched to a loudspeaker to gain maximum power transfer and, thus, maximum volume of sound.
This plays a key role in radio transmitter design, as the transmission line or antenna’s impedance must be matched exactly to the final power of an amplifier for maximum radio frequency output.
Unmatched Conditions: The Inefficient Circuit
While accurate, balanced impedance matching can lead to the desired maximum power transfer in some instances, an unmatched system can lead to loss. Excessive power loss, heat dissipation, and even circuit failure can all result from improper impedance matching. In these cases, reduced efficiency is a result of improper matching, which causes excessive power loss.
For example, in transmission lines, impedance is matched to prevent reflection. Reflection of signal in transmission lines leads to addition power waste, and frequency-dependent loss occurs. In these instances, decreased efficiency is not directly linked to impedance mismatching, but is due to additional power loss caused by reflection, which is a consequence of impedance mismatch. Here, power is not only being dissipated in the source and load, but also by a third power-loss factor, which causes reduced efficiency.
Impedance Matching Transformers
In cases requiring impedance matching, impedance matching transformers come into play.
Impedance matching transformers are designed to provide maximum power transfer from source to load, altering circuit impedances to allow for necessary matching. By applying an appropriate turns ratio to the ratio of load impedance to output impedance, these devices translate resistance on one side of the circuit into the required value on the other side.
To illustrate this further, let’s take the example of a tube amplifier. Tubes give their highest power at fairly high voltages (300-400 volts) and low currents, while most speakers need much more current at much lower voltages. For example, 128 watts of power into an 8 ohm speaker requires 32 volts (V) at 4 amps (A). If the output from the tube is 384 V, only 0.333 amps is required to support 128 watts. The impedance of the speaker is 32 V / 4 A = 8 ohms; the impedance of the amp is 384 V / 0.333 A = 1152 ohms. For maximum power transfer, we need to “match” 8 ohms to 1152 ohms. We can do this using a transformer to reduce the voltage by a factor of 12 (from 384 V down to 32 V) and proportionally increasing the current by a factor of 12 (from 0.333 A to 4 A). These transformers are particularly useful when dealing AC voltages. Note that the impedance ratio of 1152:8 ohms (144:1 ratio) is exactly the square of the voltage ratio of 384:32 volts (12:1 ratio).
Efficient Solutions from Triad Magnetics
The team at Triad Magnetics offers innovative custom magnetics design and engineering services, all backed by ISO 9001:2015 certification. We maintain a stock catalog of over 1,000 parts and can custom-design solutions as needed — whether clients require switch-mode/high-frequency or wall plug-in options, power transformers, inductors, or audio transformers. And with over 50 years of experience, we’re proud to be leaders in the field.
To learn more about the importance of the maximum power transfer theorem and how to reliably balance circuit impedance, check out our new eBook, “Impedance Matching Transformers.” And if you have any questions about and of our transformers, contact us or request a quote today!







